Vektor

Vektorer är matematiska storheter som har både storlek (magnitud) och riktning. De används därför ofta för att beskriva fysikaliska storheter med magnitud och riktning i rummet, som till exempel kraft, hastighet, acceleration, elektriskt fält och magnetfält. Sådana vektorer kallas även rumsvektorer eller geometriska vektorer. Ibland studeras rumsvektorer även i två dimensioner. I motsats till vektorstorheter är storheter som temperatur och ljusstyrka skalärer då de saknar riktning.

Inom matematiken generaliseras vektorer till att vara element i ett vektorrum av godtycklig dimension. En sådan generaliserad vektor kan ha en norm som anknyter till längdbegreppet. För vektorrummet kan en inre produkt vara definierad vilken kan sägas mäta vinklar mellan vektorerna. Med denna definition kan många typer av objekt anses vara vektorer. Det enda kravet är att de följer de viktigaste av de räkneregler som gäller för rumsvektorer.

Historik

Vektorbegreppet, såsom vi känner det idag, utvecklades gradvis över en period av mer än 200 år. Omkring ett dussin personer gjorde signifikanta bidrag.

Giusto Bellavitis abstraherade den grundläggande idén 1835 när han etablerade begreppet ekvipollens. Han studerade det euklidiska planet och definierade som ekvipollenta (likvärdiga) varje par av linjesegment av samma längd och riktning. Väsentligen upptäckte han en ekvipollensrelation för paren av punkter (tvåpunkter) i planet och skapade därmed det första vektorrummet i planet.

Termen vektor introducerades av William Rowan Hamilton som en del av en kvaternion, vilken är en summa q = s + v av ett reellt tal s (också kallat skalär) och en 3-dimensionell vektor v. Liksom Bellavitis, betraktade Hamilton vektorer som en representation av klasser av ekvipollent riktade linjesegment. I analogi med komplexa tal, som använder en imaginär del för att komplettera den reella tallinjen, betraktade Hamilton vektordelen v som den imaginära delen av en kvaternion.

Flera andra matematiker utvecklade vektorliknande system under 1800-talets mitt, däribland Augustin Louis Cauchy, Hermann Grassmann, August Möbius, Comte de Saint-Venant och Matthew O'Brien . Grassmanns arbete från 1840 Theorie der Ebbe und Flut var det första systemet av rumslig analys som liknade dagens system och presenterade idéer som motsvarar kryssprodukt, skalärprodukt och vektordifferentiering. Grassmanns arbete uppmärksammades först i slutet av 1870-talet.

Peter Guthrie Tait fortsatte att arbeta med kvaternioner efter Hamilton. Hans Elementary Treatise of Quaternions från 1870 inkluderade en utförlig behandling av nablaoperatorn ∇.

1878 publicerades Elements of Dynamic av William Kingdon Clifford, ett verk som förenklade studiet av kvaternionen genom att isolera skalärprodukten och kryssprodukten av två vektorer från den kompletta kvaternionprodukten, vilket gjorde vektorberäkningar tillgängliga för ingenjörer och andra som arbetade i tre dimensioner och var skeptiska till den fjärde.

Josiah Willard Gibbs, som stötte på kvaternioner genom James Clerk Maxwells Treatise on Electricity and Magnetism, skilde av deras vektordel för en oberoende behandling. Den första halvan av Gibbs Elements of Vector Analysis, publicerad 1881, presenterade vad som väsentligen är det moderna systemet för vektoranalys. 1901 publicerade Edwin Bidwell Wilson Vector Analysis, som i huvudsak var tillämpningar hämtade från Gibbs föreläsningar och som övergav allt omnämnande av kvaternioner.

Vektorbeteckningar

Ett vektornamn skrivs vanligen med fet stil, till exempel som

$\mathbf {a}$

I vissa fall kan även notationen

${\overrightarrow {AB}}$

förekomma där A är vektorns startpunkt och B dess ändpunkt.

Andra vanliga notationer är

${\vec {a}},\ \mathbf {\hat {a}}$

där en pil eller "hatt" placerats ovanför namnet.

Representation av vektorer

En 2-dimensionell vektor bestämd av positionen av punkten A med koordinaterna (2, 3)

En 3-dimensionell vektor bestämd av basvektorerna i, j, k

En vektor är inte bunden till en position och det är därför tillåtet att förlägga en vektors startpunkt i origo i det aktuella koordinatsystemet; en konvention som ger en kompakt koordinatlista. Vektorer i ett n-dimensionellt rum ℝⁿ kan då representeras av en lista med koordinaterna för vektorernas ändpunkter enligt

$\mathbf {a} =(a_{1},\ a_{2},\dots ,\ a_{n})$

Talen i listan kallas också vektorns komponenter. I enlighet med figuren till höger kan den 2-dimensionella vektorn från O = (0, 0) till A = (2, 3) skrivas som

$\mathbf {a} =(2,\ 3)$

En vektor kan också beskrivas genom att koordinatlistor anges för både start- och ändpunkter.

I ℝ³ identifieras vektorer med tripplar av koordinater:

$\mathbf {a} =(a_{1},\ a_{2},\ a_{3})$

eller

$\mathbf {a} =(a_{x},\ a_{y},\ a_{z})$

Ibland arrangeras dessa tripplar till kolonnvektorer eller radvektorer, särskilt i samband med hantering av matriser:

$\mathbf {a} ={\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\\\end{bmatrix}}$

$\mathbf {a} =[a_{1}\ a_{2}\ a_{3}]$

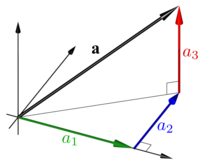
Ett annat sätt att representera vektorer är att introducera standardbasvektorer, vilket i det tredimensionella fallet kräver tre vektorer. Standardbasvektorerna har längden 1 och riktningar som sammanfaller med riktningarna för koordinatsystemets (kartesiskt) tre axlar:

${\mathbf {e} }_{1}=(1,\ 0,\ 0),\ {\mathbf {e} }_{2}=(0\ ,1\ ,0),\ {\mathbf {e} }_{3}=(0,\ 0,\ 1)$

Med hjälp av standardbasvektorerna kan varje vektor skrivas som

$\mathbf {a} =\mathbf {a} _{1}+\mathbf {a} _{2}+\mathbf {a} _{3}=a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3}$

I elementära läroböcker i fysik betecknas ofta basvektorerna med $\mathbf {i} ,\ \mathbf {j} ,\ \mathbf {k}$ (eller $\mathbf {\hat {x}} ,\ \mathbf {\hat {y}} ,\ \mathbf {\hat {z}}$, där ^ vanligtvis betecknar enhetsvektorn). I detta fall betecknas vektorkoordinaterna enligt a_x, a_y, a_z, och a_x, a_y, a_z. Således,

$\mathbf {a} =\mathbf {a} _{x}+\mathbf {a} _{y}+\mathbf {a} _{z}=a_{x}{\mathbf {i} }+a_{y}{\mathbf {j} }+a_{z}{\mathbf {k} }$

För vektorer kan basbyten utföras och nya vektorer kan användas som bas. En vektor kan transformeras till att representeras i vilken som helst av dessa nya baser.

Egenskaper

Identiska vektorer

Två vektorer är identiska om vektorerna har samma storlek och riktning. De två vektorerna

${\mathbf {a} }=a_{1}{\mathbf {e} }_{1}+a_{2}{\mathbf {e} }_{2}+a_{3}{\mathbf {e} }_{3}$

och

${\mathbf {b} }=b_{1}{\mathbf {e} }_{1}+b_{2}{\mathbf {e} }_{2}+b_{3}{\mathbf {e} }_{3}$

är identiska om och endast om

$a_{1}=b_{1},\quad a_{2}=b_{2},\quad a_{3}=b_{3}$

Addition och subtraktion

Summan av två vektorer

$\mathbf {a} =(a_{1},a_{2},a_{3}),\mathbf {b} =(b_{1},b_{2},b_{3})$

är

$\ \mathbf {a} +\mathbf {b} =(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3})$

Den resulterande vektorns komponenter är de komponentvisa summorna av vektorernas komponenter vilket kan generaliseras till alla dimensioner.

Differensen mellan a och b är

$\mathbf {a} -\mathbf {b} =(a_{1}-b_{1},a_{2}-b_{2},a_{3}-b_{3})$

Subtraktionen a - b kan tolkas som additionen a + -b.

Skalär multiplikation

De skalära multiplikationerna −a och 2a av en vektor a

Om en vektor multipliceras med ett reellt tal r (en skalär) ändras vektorns längd (skalning av vektorn):

$\ r\mathbf {a} =r(a_{x},a_{y},a_{z})=(ra_{x},ra_{y},ra_{z})$

Om r är negativ kastas vektorns riktning om, det vill säga, vektorn roteras 180°.

Skalär multiplikation är distributiv över vektoraddition

r(a + b) = ra + rb

för alla vektorer a och b och alla skalärer r.

Längd

Längden eller magnituden eller normen av vektorn a betecknas ||a||.

Längden av vektorn a kan i ett vektorrum med euklidisk norm beräknas med Pytagoras sats enligt

$\left\|\mathbf {a} \right\|={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}$

då koordinataxlarna är vinkelräta mot varandra i detta vektorrum.

Normen är även lika med kvadratroten ur skalärprodukten (se nedan) av vektorn med sig själv:

$\left\|\mathbf {a} \right\|={\sqrt {\mathbf {a} \cdot \mathbf {a} }}$

Vektorer med längden 1 kallas enhetsvektorer och nollvektorn har längden noll. Normalisering av en vektor a = [a₁, a₂, a₃], sker genom att vektorn multipliceras med det reciproka värdet av vektorns längd, ||a||:

$\mathbf {\hat {a}} ={\frac {\mathbf {a} }{\left\|\mathbf {a} \right\|}}={\frac {a_{1}}{\left\|\mathbf {a} \right\|}}\mathbf {e} _{1}+{\frac {a_{2}}{\left\|\mathbf {a} \right\|}}\mathbf {e} _{2}+{\frac {a_{3}}{\left\|\mathbf {a} \right\|}}\mathbf {e} _{3}$

Skalärprodukt

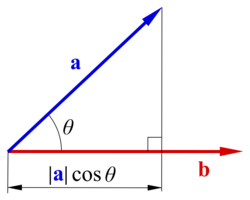
Skalärprodukten av två vektorer a och b (ibland kallad inre produkt) betecknas a ∙ b och dess resultat är en skalär (ett reellt tal, här en längd multiplicerad med en längd) och är definierad som

$\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta$

där θ är mätetalet för vinkeln mellan a och b. Geometriskt innebär detta att a och b kan antas dragna från en gemensam startpunkt och längden av projektionen av a på b är multiplicerad med b:s längd.

Skalärprodukten kan i ett ortonormerat koordinatsystem definieras som summan av de komponentvisa produkterna enligt

$\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\dots +a_{n}b_{n}$

Skalär trippelprodukt

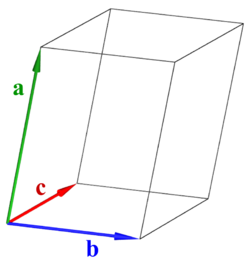
Skalära trippelprodukten definieras som skalärprodukten av en vektor och kryssprodukten (se nedan) av två andra vektorer:

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )$

Trippelprodukten kan geometriskt tolkas som volymen av en parallellipiped som spänns upp av de tre vektorerna.

Trippelprodukten kan beräknas enligt

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )$

Om vektorerna i kryssprodukten byter plats negeras trippelprodukten:

$\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )=-\mathbf {c} \cdot (\mathbf {b} \times \mathbf {a} )$

Den skalära trippelprodukten kan också tolkas som determinanten till en 3 × 3 matris som har tre vektorer som rader eller kolumner (transponering av en matris ändrar inte determinantens värde):

$\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\det {\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\\\end{bmatrix}}$

Kryssprodukt

Kryssproduktens magnitud är lika med arean av parallellogrammen som spänns upp av a och b. n är normalvektor till både a och b

Högerhandsregeln för en kryssprodukt.

Kryssprodukten (också kallad vektorprodukt eller yttre produkt) är bara meningsfull i tre eller sju dimensioner. Kryssprodukten skiljer sig från skalärprodukten genom att resultatet är en vektor. Kryssprodukten, betecknad a × b, är en vektor vinkelrät mot både a och b och definieras som

$\mathbf {a} \times \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\sin(\theta )\,\mathbf {n}$

där θ är mätetalet för vinkeln mellan a och b, och n är en enhetsvektor vinkelrät mot både a och b som tillsammans med dessa bildar ett högerorienterat system.

Längden av a × b kan tolkas som arean av en parallellogram som har a och b som sidor.

Kryssprodukten kan i ett ortonormerat koordinatsystem också skrivas som

${\mathbf {a} }\times {\mathbf {b} }=(a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1})$

Kryssprodukten är antikommutativ:

$\mathbf {a} \times \mathbf {b} =-\mathbf {b} \times \mathbf {a}$

Den är distributiv för addition:

$\mathbf {a} \times (\mathbf {b} +\mathbf {c} )=(\mathbf {a} \times \mathbf {b} )+(\mathbf {a} \times \mathbf {c} )$

Kryssprodukten är relaterad till skalärprodukten enligt

$\left\|\mathbf {a} \times \mathbf {b} \right\|^{2}=\left\|\mathbf {a} \right\|^{2}\left\|\mathbf {b} \right\|^{2}-(\mathbf {a} \cdot \mathbf {b} )^{2}$

Vektoriell trippelprodukt

Den vektoriella trippelprodukten är kryssprodukten av en vektor och kryssprodukten av två andra vektorer:

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \,(\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} \,(\mathbf {a} \cdot \mathbf {b} )$.

Då kryssprodukten är antikommutativ kan detta också skrivas

$(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =-\mathbf {c} \times (\mathbf {a} \times \mathbf {b} )=-(\mathbf {c} \cdot \mathbf {b} )\,\mathbf {a} +(\mathbf {c} \cdot \mathbf {a} )\,\mathbf {b}$

En annan användbar formulering är

$(\mathbf {a} \times \mathbf {b} )\times \mathbf {c} =\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )\;-\mathbf {b} \times (\mathbf {a} \times \mathbf {c} )$

Vektorprojektion

Projektion av a på b (a₁). När 90° < θ ≤ 180°, har a₁ en motsatt riktning med avseende på b

Projektionen av en vektor a på en vektor b (en vektorkomponent i b:s riktning) är den ortogonala projektionen av a på en rät linje parallell med b och definieras som

$\mathbf {a} _{1}=a_{1}\mathbf {\hat {b}}$

där $a_{1}$ är en skalär, kallad den skalära projektionen av a på b och b̂ är enhetsvektorn i b:s riktning. Den skalära projektionen definieras i sin tur som

$a_{1}=|\mathbf {a} |\cos \theta =\mathbf {a} \cdot \mathbf {\hat {b}} =\mathbf {a} \cdot {\frac {\mathbf {b} }{|\mathbf {b} |}}$

där operatorn · betecknar skalärprodukt, |a| är den euklidiska normen av a och θ är vinkeln mellan a och b. Den skalära projektionen har samma längd som vektorprojektionen.

Vektorkomponenten a₂ av a vinkelrät mot b är

$\mathbf {a} _{2}=\mathbf {a} -\mathbf {a} _{1}.$

När vinkeln θ är okänd kan cosinus θ beräknas med hjälp av a och b och definitionen av skalärprodukt:

${\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\,|\mathbf {b} |}}=\cos \theta$

Med hjälp av denna egenskap blir definitionen av den skalära projektionen

$a_{1}=|\mathbf {a} |\cos \theta =|\mathbf {a} |{\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\,|\mathbf {b} |}}={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {b} |}}\,$

På liknande sätt blir definitionen av a:s vektorprojektion på b

$\mathbf {a} _{1}=a_{1}\mathbf {\hat {b}} ={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {b} |}}{\frac {\mathbf {b} }{|\mathbf {b} |}},$

vilket är ekvivalent med endera

$\mathbf {a} _{1}=(\mathbf {a} \cdot \mathbf {\hat {b}} )\mathbf {\hat {b}} ,$

eller

$\mathbf {a} _{1}={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {b} |^{2}}}{\mathbf {b} }={\frac {\mathbf {a} \cdot \mathbf {b} }{\mathbf {b} \cdot \mathbf {b} }}{\mathbf {b} }$

Exempel

Avståndet PQ mellan två linjer kan bestämmas genom en projektion av $\mathbf {v}$ på linjernas normalvektor $\mathbf {n}$. Linjerna ligger i två parallella plan som är bestämda av normalvektorn $\mathbf {n}$ och av punkterna P och Q som ligger i respektive plan

Bestäm avståndet mellan två linjer i R³ givna i parameterformerna

$(1,\ 1,\ 1)+t(1,\ 2,\ 1)$

$(1,\ 3,\ 4)+t(2,\ 2,\ 0)$

där riktningsvektorerna för linjerna är

$\mathbf {u} _{1}=(1,\ 2,\ 1)$

$\mathbf {u} _{2}=(2,\ 2,\ 0)$

Kortaste avståndet representeras av en sträcka d = PQ som är ortogonal mot linjerna. Vektorn $\mathbf {n} =\mathbf {u} _{1}\times \mathbf {u} _{2}$ är linjernas normalvektor med samma riktning som sträckan PQ. En vektor $\mathbf {v}$ för linjen mellan linjernas fixa punkter är

$\mathbf {v} =(1,\ 3,\ 4)-(1,\ 1,\ 1)=(0,\ 2,\ 3)$

Avståndet d mellan linjerna är projektionen av $\mathbf {v}$ på $\mathbf {n}$:

$d=|\mathbf {v} \cdot {\cfrac {\mathbf {n} }{\|\mathbf {n} \|}}|={\cfrac {1}{\sqrt {3}}}={\cfrac {\sqrt {3}}{3}}$

Vektorer i ℝ² och komplexa tal

Komplexa tal kan ses som ett fall av vektorer i ℝ². Ett komplext tal har en realdel och en imaginärdel som kan representeras som komponenter i en vektor och som även kan ritas som en vektorpil i det komplexa talplanet. Addition, subtraktion, skalning och längdberäkning utförs som för rumsliga vektorer i ℝ². Komplexa tal medger dessutom vanlig multiplikation och division.

En annan förbindelse mellan komplexa tal och vektorer är vektorer vars komponenter är komplexa tal (komplexvärda vektorer).

Vektorfält

Ett vektorfält är en tilldelning av en vektor till varje punkt i en delmängd av rummet.

• 
  En del av vektorfältet (sin y, sin x)
• 
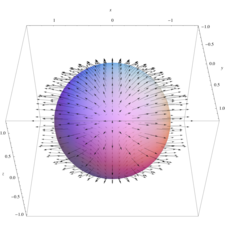
  Ett vektorfält på en sfär
• 
  Vektorfält runt ett flygplan, visualiserat med bubblor

Exempel på vektorfält:

• Gradientfält
• Divergensfält
• Rotationsfält
• Skalärpotential, gradientens invers

Se även

• Enhetsvektor
• Kontravariant vektor
• Kovariant vektor
• Kovarians och kontravarians (vektorer)
• Linjärt rum (vektorrum)
• Normalvektor
• Ortsvektor
• Poyntings vektor
• Pseudovektor (axiell vektor)
• Rumsvektor
• Talföljd
• Vektoranalys

Referenser

• Folke Eriksson, Flerdimensionell Analys, Studentlitteratur Lund 1971

Vidare läsning

• Gavel, Hillevi (2011). Grundläggande linjär algebra. Studentlitteratur. Libris 12242337. ISBN 9789144076058 
• Sparr, Gunnar, 1942- (1995 ;). Linjär algebra. Studentlitteratur. OCLC 187001658. http://worldcat.org/oclc/187001658. Läst 15 juni 2019 
• Månsson, Jonas.. Linjär algebra.. ISBN 9789144127408. OCLC 1097632984. http://worldcat.org/oclc/1097632984. Läst 15 juni 2019 

Externa länkar

• Wikimedia Commons har media som rör Vektor.
  Bilder & media